四年级上册数学重点知识点整理

第一单元：大数的认识

一、亿以内数的认识

1. 数位与数级

   • 数位：在用数字表示数的时候，这些计数单位要按照一定的 顺序 排列起来，它们所占的位置叫做 数位 。

   • 数级：按照我国的计数习惯， 每四个数位是一级 。

     个位、十位、百位、千位是个级；

     万位、十万位、百万位、千万位是万级；

     亿位、十亿位、百亿位、千亿位是亿级。

2. 亿以内数的读法

   • 先读万级，再读个级；

   • 万级的数都要按照个级的数的读法来读，再在后面加上一个“万”字；

   • 每级末尾不管有几个0，都 不读 ，其他数位有一个0或连续几个0，都 只读一个“零” 。

     例：7806009，读作：七百八十万六千零九

3. 亿以内数的写法

   • 先写万级，再写个级；

   • 哪个数位上一个单位也没有，就在那个数位上写0。

     例：三百零二万六千写作：3026000

4. 亿以内数的大小比较

   • 位数 不同时 ，位数 多的数大 ；

   • 位数 相同时 ，从最高位比起， 最高位 的数 大 的那个数就 大 ，如果最高位上的数 相同 ，就比较 下一个 数位上的数，直到比较出大小为止。

     例：506012＞50601；506012＜506022

5. 整万的数改写成用“万”作单位的数:

   • 去掉末尾的4个0，再加上“万”字（目的是为了读写方便）。

     例：200000=20万

6. 不是整万的数改写成“万”作单位的近似数:

   • 要将 “千位” 上的数四舍五入，然后再加上 “万” 字。

     例：53850≈50000=5万；57220≈60000=6万

7. 四舍五入法:

   求一个数的近似数，要先看省略的尾数部分的最高位是小于5，还是等于或大于5：

   如果 小于5 就把它和后面的尾数全部舍去，改写成 0 ；

   如果 等于或大于5 就先向前一位 进1 ，再把它和后面的尾数全部舍去，改写成 0 。

   这种求近似数的方法叫做四舍五入法。

二、数的产生

1. 数：是应人们生产生活的需要而产生的。最初有实物记数、结绳记数、刻道记数，后出现了记数符号（即数字）。阿拉伯数字是现今世界通用的数字，它是印度人发明的。

2. 自然数：表示物体个数的0、1、2、3、4、5、6、7、8、9、10、11……都是自然数。

最小的自然数是0，没有最大的自然数，自然数的个数是无限的。

三、十进制计数法

1. 计数单位：个（一）、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿都是计数单位。每相邻两个计数单位间的进率都是10。

2. 十进制计数法：每相邻两个计数单位之间的进率都是十的计数方法叫做十进制计数法。

四、亿以上数的认识

1. 亿以上数的读法

   • 先分级，再从最高级读起；

   • 读完亿级或万级的数，要加“亿”字或“万”字；

   • 每级末尾不管有几个0，都不读，其他数位有一个0或连续几个0，都只读一个“零”。

   例：208007806003读作：二千零八十亿零七百八十万六千零三

2. 亿以上数的写法

   • 先看这个数有几级，再从最高级写起；

   • 哪个数位上一个单位也没有，就在那个数位上写0。

3. 整亿数改写成用“亿”作单位的数

   • 先分级，找到亿位，去掉末尾的8个0，再加上一个“亿”字。

   例：500000000=5亿

4. 不是整亿的数改写成“亿”作单位的近似数

   • 要将“千万位”上的数四舍五入，然后再加上“亿”字。

   例：5132207500≈5亿；7153293850≈72亿

五、计算工具的认识和应用

1. 计算工具的发展

   • 二千多年前，中国人用算筹计算；

   • 一千多年前，中国人又发明了算盘；

   • 17世纪初，英国人发明了计算尺；

   • 17世纪中期，欧洲人发明了机械计算器；

   • 20世纪，出现了电子计算器；

   • 20世纪40年代，诞生了第一台电子计算机。

2. 算盘的认识

   • 算盘各部分名称：

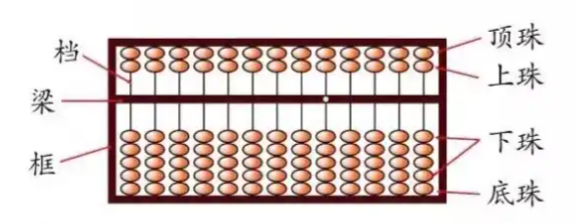
   • 算盘的主要作用是计算和计数。

   • 计数规则：

     • 每一个档代表一个数位，计数前要先选定一个档作为个位，然后向左依次是十位、百位……

     • 一个下珠表示1，一个上珠表示5；

     • 拨数时，要把珠子拨到靠梁时，才表示算盘上有数。

   • 特殊情况：根据计算的需要，有的算盘没有顶珠和底珠。

3. 计算器的认识

   • 计算器组成：

   显示屏、数字键、运算符号键（+、-、×、÷）、清零键（AC）、清除键（CE）、存储运算键（+/ -、FB、HX）、关机/清屏键（ON）

• 数位表

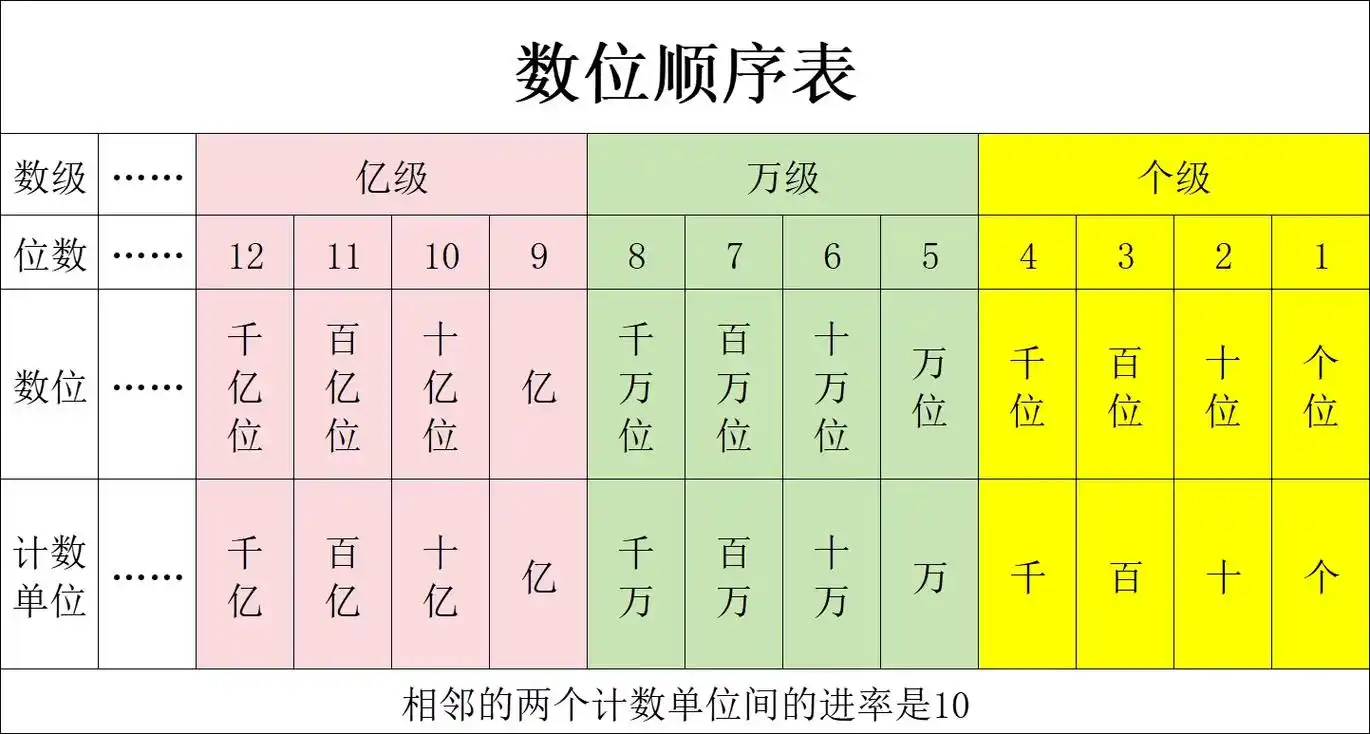
第二单元：公顷和平方千米

一、公顷和平方千米

1. 公顷

   • 适用场景：测量土地的面积可以用“公顷”（ha）作单位。

   • 定义： 边长是100米的正方形面积是1公顷 。

   • 单位换算：(1 公顷 =10000 平方米 )

2. 平方千米

   • 适用场景：计量比较大的土地面积，常用“平方千米”（km²）作单位。

   • 定义：边长是1千米的正方形面积是1平方千米。

   • 单位换算：(1 平方千米 = 1000000 平方米 = 100 公顷)

3. 拓展：测量土地面积常用的单位还有 公亩、亩和平方公里 。

   • 1公顷=100公亩

   • 1公顷=15亩

   • 1平方千米=1平方公里

第三单元：角的度量

一、线段、直线、射线

1. 特点和区别

   • 线段：有两个端点，不能延伸，有一定的长度，可以测量；

   • 射线：只有一个端点，可以向一端无限延伸，是无限长的，无法测量；

   • 直线：没有端点，可以向两端无限延伸，是无限长的，无法测量。

2. 表示方法

   • 线段、直线、射线都可以用字母表示。
   • 例：

   (1)线段AB，长5厘米；

   

   (2)把线段AB向一端无限延伸，得到射线BA或射线AB（读射线时，先读端点）；

   

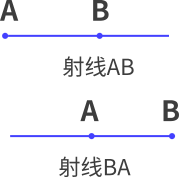
   (3)把线段AB向两端无限延伸，得到直线AB，还可以用小写字母表示（如直线a）。

   

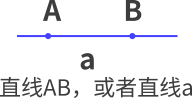
3. 拓展

   • 过一点能画无数条直线，过两点只能画一条直线；

   • 线段、直线、射线都是直的，线段和射线是直线上的一部分。

二、角的定义

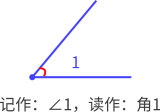
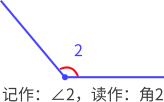
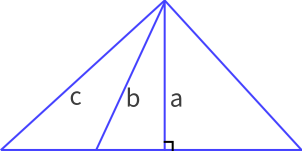
• 从一点引出两条射线所组成的图形叫做角。
• 各部分名称：这个点叫做角的顶点，这两条射线叫做角的两条边（角由 一个顶点和两条边 组成）。
• 表示方法：角通常用符号“∠”表示，如图中角可以记作“∠1”。

三、角的度量

1. 度量单位：角的度量单位是“度”（°）。

   • 定义：人们将圆平均分成 360份 ，将其中 1份 所对的角作为 度量 角的单位，它的大小就是 1度 ，记作 1° 。

2. 度量工具：量角器（又叫半圆仪）。

   • 量角器结构：刻度线、刻度中心点、零刻度线；
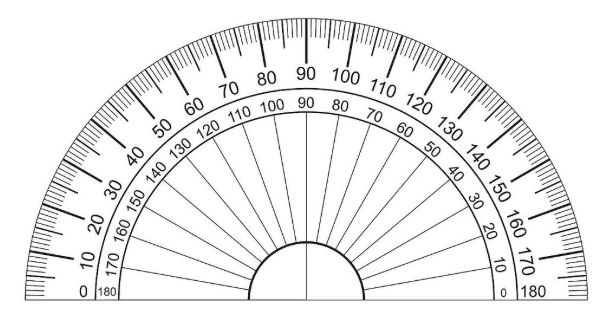
   • 制作原理：把半个圆分成 180等份 制成。

3. 拓展：角的单位有 度、分、秒 ;

   换算关系为:$1^{\circ }={60}^{\prime }$ ，$1^{\prime }={60}^{″}$。

四、角的分类

1. 各类角的度数

   • 直角：1 直角 = ${90}^{\circ }$
   • 平角：1 平角 =${180}^{\circ }$
   • 周角：1 周角 =${360}^{\circ }$
   • 锐角：锐角 <${90}^{\circ }$
   • 钝角：${90}^{\circ }$ < 钝角 < ${180}^{\circ }$

2. 角的数量关系

   • 平角 =2个 直角

   • 周角 = 2个平角 = 4个直角

3. 角的大小关系：锐角 < 直角 < 钝角 < 平角 < 周角

4. 角的大小影响因素：

   角的大小与角的两边画出的 长短没关系 ，要看两条边 叉开 的大小， 叉开得越大 ， 角越大 。

五、画角

1. 量角口诀：“两重一看”

   • 量角器的 中心 和 射线 的端点 重合 ；

   •  0°刻度线 与所画的 射线 重合；

   •  看准刻度 。

2. 画角步骤

   • 第一步：画一条射线，使量角器的中心和射线的端点重合，0°刻度线和射线重合；

   • 第二步：在量角器上找到对应刻度线（如65°）的地方点一个点；

   • 第三步：以画出的射线的端点为端点，通过刚画的点，再画一条射线。

第四单元：三位数乘两位数

一、笔算乘法

1. 多位数乘两位数的笔算步骤

   • 第一步：从低位到高位，用两位数每一位上的数去乘多位数；

   • 第二步：用两位数哪一位上的数去乘，乘得的积的末位就要和那一位对齐；

   • 第三步：把两次乘得的积加起来。

     例：计算138×38

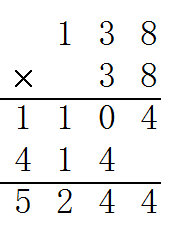
     • 先算个位上的8乘以138等于1104，1104和个位对齐；
     • 再算十位上的3乘以138等于414，414和十位对齐；
     • 最后，两得数相加：1104 + 4140 = 5244。

2. 因数末尾有0的乘法

   • 方法：可以先把0前面的数 相乘 ，再看 因数末尾一共有几个0 ，就在乘得的积的 末尾 添几个0。

3. 因数中间有0的乘法

   • 注意事项：计算时应注意用两位数去乘三位数时，三位数 中间的0 也要乘，然后再加上 进上来 的数。

二、积的变化规律

• 两数相乘，一个因数 XXX 不变，另一个 因数 乘（或除以）几（0除外）， 积也乘（或除以）几 。

三、数量关系

1. 单价、数量、总价

   • 定义：
     • 每件商品的价钱叫做 单价 ；
     • 买了多少叫做 数量 ；
     • 一共用的钱数叫做 总价 。
   • 数量关系式：

     • 单价×数量 = 总价

     • 总价÷单价 = 数量

     • 总价÷数量 = 单价

2. 速度、时间、路程

   • 定义：
     • 一共行了多长的路叫做 路程 ；
     • 每小时（或每分钟等）行的路程叫做 速度 ；
     • 行了几小时（或分钟等）叫做 时间 。
   • 数量关系式：

     • 速度×时间 = 路程

     • 路程÷时间 = 速度

     • 路程÷速度 = 时间

第五单元：平行四边形和梯形

一、平行与垂直

1. 同一平面内两条直线的位置关系： 平行或相交 。

2. 平行

   • 定义：在同一个平面内，不相交的两条直线叫做 平行线 ，也可以说这两条直线 互相平行 。
   • 表示方法：直线a平行于直线b，记作“a∥b”，读作“a平行于b”。

3. 垂直

   • 定义：两条直线相交成 直角 ，就说这两条直线 互相垂直 ，其中一条直线叫做另一条直线的 垂线 ，这两条直线的交点叫做 垂足 。
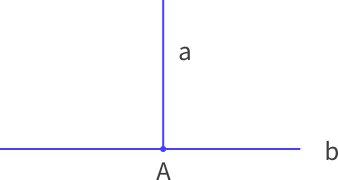
   • 表示方法：直线a垂直于直线b，记作“a⊥b”，读作“a垂直于b”，点A就是垂足。

4. 画垂线的方法

①过直线上一点画这条直线的垂线：

     把三角尺的一条直角边靠近直线，三角尺上的直角顶点靠近直线上的点，然后用笔沿另一条直角边画出
     直线（射线），在垂足处标出垂直符号。

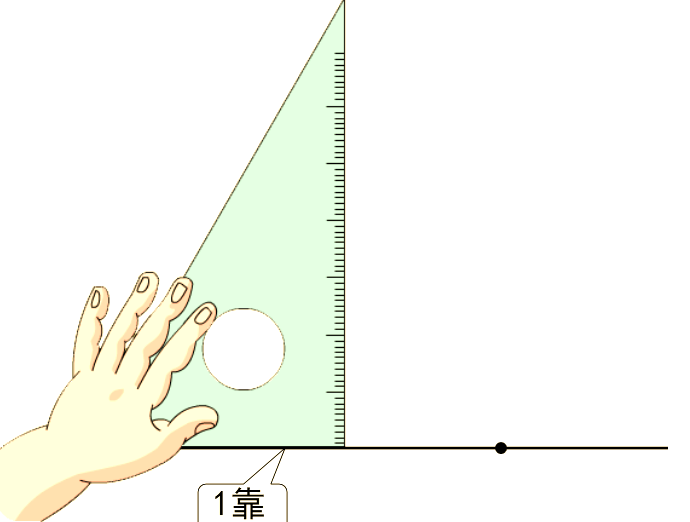
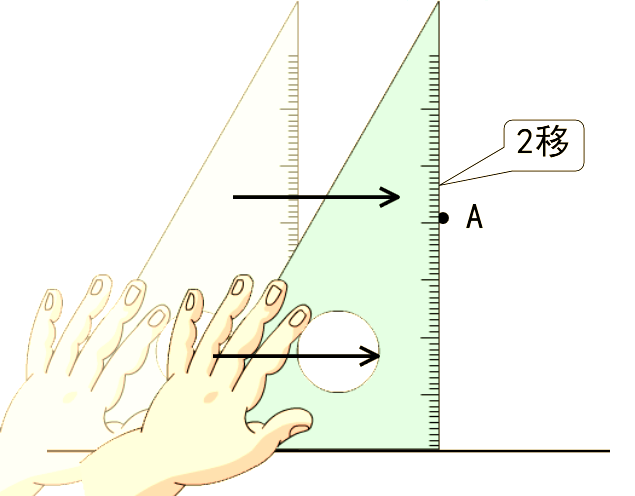
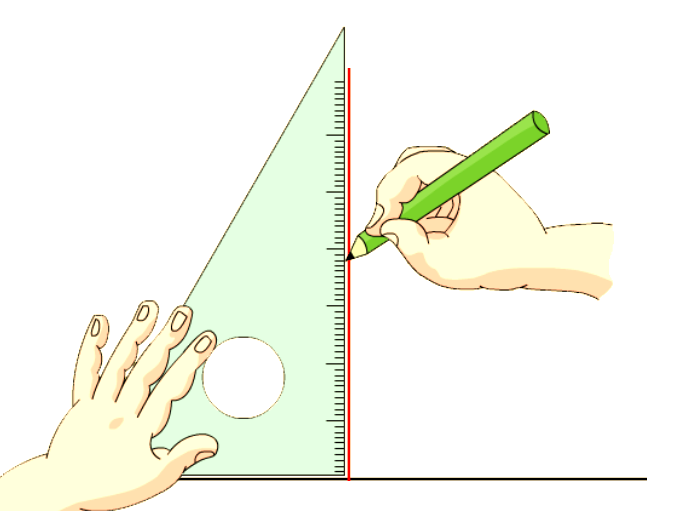
②过直线外一点画这条直线的垂线：

    把三角尺的一条直角边靠近直线，三角尺上的另一条边靠近直线外的点，然后用笔沿这条边
    画直线（射线），在垂足处标出垂直符号。

③工具选择：

    可以利用三角尺或量角器画垂线。

5. 距离

   • 定义：

     从直线外一点到这条直线所画的垂直线段 最短 ，它的长度叫做这点到直线的 距离 。

   例：点A到直线所画的垂直线段最短，线段a最短。

6. 画长方形：

    可以用画垂线的方法来画长方形
   
    先画一条长，再沿长的两端画垂线作为宽，最后连接宽的端点。
   

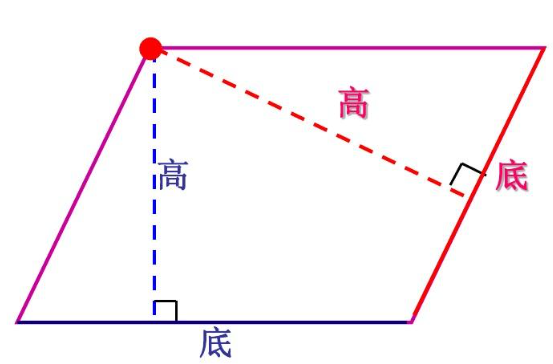
二、平行四边形的认识

1. 定义：

    两组 对边分别 互相平行 的四边形叫做 平行四边形 。

2. 高和底

   • 从平行四边形一条边上向对边引一条 垂线 ，这点和垂足之间的线段叫做平行四边形的 高 ；
   • 垂足所在的边叫做平行四边形的 底 ；
   • 平行四边形有 无数条高 ，一个平行四边形能画出 两组 不同的高。

3. 特性：平行四边形有 容易变形 的特点（可用于制作 伸缩门 等）。

三、梯形的认识

1. 定义：

   只有 一组 对边 互相平行 的四边形叫做 梯形 。

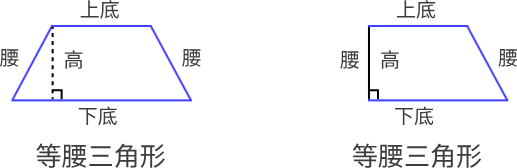
2. 各部分名称

   • 平行的一组对边中， 较短 的边是 上底 ， 较长 的边是 下底 ；
   •  不平行 的一组对边叫 腰 ；
   • 梯形上、下底间的垂直线段叫梯形的 高 。

3. 特殊梯形

   • 等腰梯形： 两个腰相等 的梯形；
   • 直角梯形： 有一个角是直角 的梯形。

四、四边形的集合（关系）

 平行四边形 、 长方形 、 正方形 、 梯形 都是特殊的四边形；

 长方形 、 正方形 是特殊的平行四边形；

 正方形 是特殊的长方形。

第六单元：除数是两位数的除法

一、口算除法

1. 整十数除整十数或几百几十数的口算方法

   • 方法一：想乘法做除法

     例：80÷20，想20×4=80，所以80÷20=4；

   • 方法二：去掉被除数和除数末尾相同个数的0，再计算

     例：150÷50，先把150和50同时去掉1个0，变成15÷5=3，所以150÷50=3 。

2. 除法估算

   • 方法：根据被除数和除数的特点，把不是整十数或不是几百几十的数看成与它接近的整十数或几百几十的数，再计算。

   例：
   

     83÷20≈4（把83看作80，80÷20=4）；
   

     150÷28≈5（把28看作30，150÷30=5；
   

      61÷21≈3（把61看作60，21看作20，60÷20=3）

二、笔算除法

1. 除数是整十数的笔算除法步骤（五步）

   • 一“看”：确定商的位置；

   • 二“试”：确定首先商几；

   • 三“乘减”：先乘后减确定再商几；

   • 四“比”：比较除数和余数的大小（余数必须比除数小）；

   • 五“落”：把被除数的个位落下来。

2. 试商的方法

   • 除数接近整十数的除法：一般按 “四舍五入” 法把除数看作它接近的整十数来 试商 ；
   • 除数不接近整十数的除法：可以采取除数 乘10法 、把除数看作几十五等方法来 试商 。

3. 除数是两位数的除法法则

   • 从被除数的 高位 起，先用除数试除被除数的前两位，如果比除数小，再试除前三位；
   • 除到被除数的哪一位，就在那一位上面 写商 ；
   • 每次除得的余数必须比除数 小 。

4. 商的变化规律

   •  除数不变 ，被除数乘几，商也 乘几 ；被除数 除以几 ，商也 除以几 （0除外）；
   •  被除数不变 ，除数 乘几 ，商 反而除以几 ；除数 除以几 ，商 反而乘几 （0除外）；
   • 被除数和除数都乘（或除以）一个 相同的数 （0除外）， 商不变 。

第七单元：条形统计图

一、条形统计图的组成

• 由标题、时间、纵轴（单位）、横轴（类别）、直条组成。

二、条形统计图的特点

• 从条形统计图中很容易看出数量的多少。

三、条形统计图的绘制注意事项

• 根据统计数据的 大小和特点 来 确定1格代表几 （如数据较大时1格代表5或10，数据较小时1格代表1）。

四、统计表与条形统计图的对比

• 统计表：数据详细，但不利于直观地分析问题；

• 条形统计图：能够直观反映 各个量的变化差异 ，有利于 对数据进行分析 。

第八单元：数学广角——优化

一、沏茶问题（时间优化）

1. 问题：怎样才能尽快让客人喝上茶？

2. 流程：洗水壶（1分钟）→ 接水（1分钟）→ 烧水（8分钟，同时洗茶杯、找茶叶）→ 沏茶（1分钟）

3. 核心思想：

   合理安排做事顺序，明确先做什么、后做什么，判断哪些事情可以同时做，从而优化时间，在规定时间内做更多事情。

二、烙饼问题（效率优化）

1. 条件：每次只能烙2张饼，两面都要烙，每次3分钟。

2. 烙饼方法（以最少时间为目标）

   • 烙3张饼：两张交替烙（不让锅空闲），共烙3次，总时间=3×3=9分钟；

   • 烙4张饼：两张两张地烙，需2次（每次烙2张），总时间=2×3×2=12分钟；

   • 烙5张饼：先烙2张（6分钟），再烙3张（9分钟），总时间=6+9=15分钟。

3. 总结规律

   • 烙2、4、6、8……（偶数）张饼：两张两张地烙，总时间=（张数÷2）×3×2=张数×3；

   • 烙3张饼：交替烙，总时间=9分钟；

   • 烙5、7、9、11……（大于3的奇数）张饼：先两张两张烙，最后3张交替烙，总时间=（张数-3）÷2×6 + 9=张数×3。

4. 核心原则：

   • 不让锅里出现空闲，最大限度利用锅的空间。

三、应对策略问题（“田忌赛马”案例）

1. “田忌赛马”策略表

赛次	齐王的马	田忌的马	本场胜者
第一场	上等马	下等马	齐王
第二场	中等马	上等马	田忌
第三场	下等马	中等马	田忌

2. 策略优化思路

   • 解决同一个问题可以有不同的策略，要学会寻找最优方案；

   • 比赛（或竞争）时的策略：

     a. 知己知彼，详细分析双方的情况；

     b. 想到所有可能的对策；

     c. 选择一个利多弊少的最优方案。